Guardrail Study: Reducing Wear, Reducing Replacements.
Transit systems are typically operated in dense urban areas, which frequently result in systems that contain a large number of curves with small radii that can increase wheel/rail wear and the potential for flange climb derailments.
Guardrails are used in transit systems to reduce rail wear in sharp curves and to increase the track’s resistance to flange climb derailment. Guardrails are also installed in track curves where the high rail wears rapidly, because they are considered beneficial in reducing the frequency and cost of high rail replacements.
Survey results published by the Transit Cooperative Research Program (TCRP) show that the practices of restraining rail installation are different and the design and maintenance standards vary between different transit systems. This wide variety of practices coupled with problems observed in the use of the guard/restraining rails, indicated that a detailed study of restraining rail designs and maintenance practices could be beneficial to all transit systems.
The Transportation Technology Center Inc. (TTCI) worked with TCRP to develop guidelines for the application of guard/restraining rails in transit systems, including comparisons of the following two guardrail installation designs (referred to as philosophies I and II) commonly used in transit systems.
Philosophy I
Figure 1 illustrates the “shared contact” methodology used by transit systems for guardrail installation, known as Philosophy I. The optimization methodology proposed in the previous study for optimal flangeway clearance clearly belongs to Philosophy I. With equal rates of wear, it is expected that the high rail and the guard/girder/restraining rail will wear out at the same time and be replaced during the same track maintenance period, minimizing service interruptions.
Philosophy II
As Figure 2 illustrates, there is a different guardrail installation philosophy used by transit systems, known as Philosophy II. The practice of Philosophy II is to increase the check gage dimension and track gage so that no flange contact with the high rail will occur under any combination of wear and tolerances. Then the guard/girder/restraining rail resists all the curving forces, and therefore experiences all the gage-face wear while the high rail experiences only rail head wear.
Even though the wheel/rail contact of these two philosophies starts in two significantly different situations, they ultimately end with the same situation as Philosophy I, because the high rail contact will eventually occur for Philosophy II as the guard/restraining rail gradually wears.
The obvious question is: Which philosophy is right for installing a guardrail? To answer this question, the effects of guardrail parameters on dynamic performances of various types of transit vehicles were investigated through NUCARS modeling. Guidelines for guardrail installation were proposed from the study.
EFFECT OF GUARDRAIL PARAMETER AND OPTIMIZATION
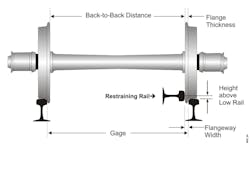
Figures 3 and 4 show typical guardrail and restraining rail structures and layouts. The geometry parameters of wheelset and track including guard/restraining rail are also labeled in the figures. The restraining rail contacts the wheel flange back flat surface with a 90-degree contact angle; the contact angle between the guardrail and wheel flange back tip depends on the rail and wheel profile shape; usually it is less than 90 degrees.
The flangeway width has the most important effect on wheel/rail forces and wear. As Figure 5 shows, for a 75-degree flange angle wheel with a 20 milliradian (mrad) yaw angle, if the flangeway width is too narrow (smaller or equal to 1.5 in.), the guardrail bears almost all the lateral force, and there is no lateral force acting on the high rail (right rail). Correspondingly, the left wheel wears severely on the guardrail, but the right wheel wear index is relatively small on the high rail tread and flange, as Figure 6 shows. The guardrail and fastener components could be damaged from the high lateral force. The guardrail service life could also be reduced from severe wear. The optimal flangeway width is 1.55 inches for the simulated case.
Simulations were also conducted to investigate effects of track gage, curve radius, guardrail height and lubrication on vehicle dynamic performances. The following conclusions can be drawn from the parametric studies:
• The optimal guard/restraining rail installation, leading to a balance of lateral wheel/rail forces as well as a balance of wear between the high rail and the guard/girder/restraining rail can be achieved through the control of flangeway width and wheel/rail friction coefficients.
• The optimal flangeway width depends on the wheel profile shape, including flange back profile, wheel back to back distance, track gage, guard/restraining rail profile shapes, installation height and wheelset angle of attack (AOA) or the track curvature.
• The flangeway width should increase with the wheelset AOA and track curvature for AOA larger than 20 mrad (corresponding to curves with about 290-foot radius) if the 3-dimensional flange back fattening effect is larger than that on the maximum flange angle face.
• The flangeway width should increase approximately the same amount as the gage increase to keep the flange front clearance equal to the flange back clearance. Increasing only the gage leads to excessive wear on the guard/girder/restraining rails.
• The flangeway width should increase with the increase of guard/restraining rail height to keep the flange front clearance equal to the flange back clearance.
• Lubrication on the high rail gage face and guard/girder/restraining rail significantly reduces the wheel/rail wear and rolling resistances. To achieve similar wear rates between the high rail and the guardrail, the guideline for rail lubrication with guardrail is to produce low friction coefficients on the contact patches in the presence of high contact angles and relative high friction coefficients on the contact patches in the presence of low contact angles.
COMPARISONS OF TWO GUARDRAIL
INSTALLATION PHILOSOPHIES
Steady-state curving simulations on a number of constant radius curves without perturbations were conducted to evaluate performance trends of the two philosophies. Two wheel/rail interaction performance indices, wheel lateral forces and wear on leading axles, were used for comparison.
Figure 7 shows more than twice the lateral force acts on just the guardrail using Philosophy II than the lateral force acts almost equally on both rails using Philosophy I.
Figure 8 shows that both philosophies resulted in a larger wear index on leading axle wheels (the sum of the wear index from all contact points on both wheels of the lead axle) than the case with no guardrail, with a lower wear index from Philosophy I than that from Philosophy II.
The simulations show that Philosophy I (shared contact between the high rail flange and the guardrail on the low rail wheel) leads to better vehicle dynamic performance than Philosophy II (no high rail flange contact and with the guardrail contact on the low rail wheel) in terms of lower lateral forces on rails, lower vehicle rolling resistance, and lower leading axle wear.
TRANSIT VEHICLE FLANGE CLIMB DERAILMENT SIMULATION
NUCARS steady-state and dynamic curving simulations of four types of transit vehicles on single cosine wave shape, with three levels of severity of perturbations, were conducted to investigate guardrail effects on increasing resistance to flange climbing derailment.
Figure 9 shows the wheel lateral to vertical (L/V) ratio on tight curves with radius less than 500 feet increases with the increase of the wheel/rail friction coefficient. The vehicle derailed on curves with radius less than or equal to 250 feet at a friction coefficient of 0.6, which indicates that a guardrail is needed even on perfect track without perturbations.
As expected, the dynamic curving L/V ratios on perturbed track without a guardrail increase with the wheel/rail friction coefficient and amplitude of the perturbations, as Figures 10 and 11 show. The dynamic L/V ratios approach or exceed the Nadal limit (shown as a solid red line) at a friction coefficient of 0.5. The vehicle derailed for all simulated cases (100 ~3,000 ft radii curves), with a friction coefficient 0.6 and the most severe track perturbations.
The following guardrail guidelines are recommended for two types (Type 1 and Type 2) of transit railcars and two types (Type 1 and Type 2) of light rail vehicles implemented with 75-degree flange angle wheels:
• For yard curves (15 mph speed limit) with the most severe track perturbations:
- No guardrails are needed for Types 1 and 2 transit railcars and Type 2 light rail vehicles.
- Guardrails should be installed on curves with radii less than or equal to 755 feet for the Type 1 light rail vehicle
• For mainline curves:
- No guardrails are needed for Types 1 and 2 transit rail cars running at 7.5 inch cant deficiency speed with Level 2 track perturbations.
- No guardrails are needed for Type 1 light rail vehicles running at 7.5 inch cant deficiency speed with Level 1 track perturbations.
- No guardrails are needed for Type 2 light rail vehicles running at 4.0 inch cant deficiency speed with Level 1 track perturbations.
- Guardrails should be installed on curves with radii less than or equal to 500 feet for Type 1 light rail vehicles running at 4-inch cant deficiency speed with Level 2 track perturbations.
- Guardrails should be installed on curves with radii greater than or equal to 955 feet for Type 2 light rail vehicles running at 4-inch cant deficiency speed with Level 2 track perturbations.
The guidelines offer guidance that transit agencies can follow in the design, construction, wheel/rail maintenance and operation of rail transit systems. Further study on guardrail for special trackwork, such as switches and frogs, is recommended to take advantage of findings from this study.
Xinggao Shu is a principal Iinvestigator with the Transportation Technology Center, Inc. (TTCI).